Differenza tra l'integrazione e la somma: l'integrazione rispetto alla somma confrontata

Integrazione vs Sommario

Nella matematica superiore della scuola superiore, l'integrazione e la sintesi si trovano spesso nelle operazioni matematiche. Essi sono apparentemente utilizzati come strumenti diversi e in situazioni diverse, ma condividono un rapporto molto stretto.

Ulteriori informazioni sulla somma

La somma è l'operazione di aggiungere una sequenza di numeri e l'operazione è spesso indicata dalla lettera greca di capitale sigma Σ. Viene usato per abbreviare la somma e uguale alla somma / totale della sequenza. Sono spesso usati per rappresentare la serie, che sono essenzialmente sequenze infinite riassunte. Possono anche essere usati per indicare la somma di vettori, matrici o polinomi.

La somma viene di solito fatta per un intervallo di valori che possono essere rappresentati da un termine generale, ad esempio una serie che ha un termine comune. Il punto di partenza e il punto finale della somma sono conosciuti rispettivamente come il limite inferiore e il limite superiore della somma., ad esempio, la somma della sequenza a ₁ , a ₂ , a ₃ , a _{4 è} 1 _{+ a} 2 _{+ a} 3 _{+ … + a} n _{che può essere facilmente rappresentato utilizzando la notazione di somma come Σ} n ^{i = 1} _a i _{; è chiamato l'indice della somma.}

Molte varianti sono utilizzate per la somma basata sull'applicazione. In alcuni casi, il limite superiore e quello inferiore possono essere dati come intervallo o un intervallo, ad esempio Σ

1≤i≤100 _a i _{e Σ} i∈ [1, 100] _a i _{. O può essere dato come un insieme di numeri come Σ} i∈P _a i _{, dove P è un set definito.}

In alcuni casi possono essere utilizzati due o più segni sigma, ma possono essere generalizzati come segue; Σ

j _a jk _{= Σ} j, k _a jk .

_{Inoltre, la somma segue numerose regole algebriche. Poiché l'operazione embedded è l'aggiunta, molte delle regole comuni di algebra possono essere applicate alle somme in sé e ai singoli termini raffigurati dalla somma.} Ulteriori informazioni sull'integrazione

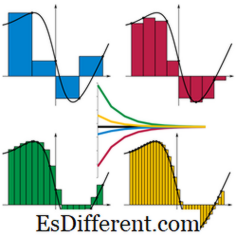
L'integrazione è definita come il processo inverso della differenziazione. Ma nella sua visione geometrica può anche essere considerata l'area racchiusa dalla curva della funzione e dell'asse. Pertanto, il calcolo dell'area dà il valore di un integrale definito come mostrato nello schema.

Immagine sorgente: // it. wikipedia. org / wiki / File: Riemann_sum_convergence. png

Il valore dell'elemento definito è in realtà la somma delle piccole strisce all'interno della curva e dell'asse.L'area di ogni striscia è l'altezza x larghezza al punto sull'asse considerato. La larghezza è un valore che possiamo scegliere, diciamo Δx. E l'altezza è approssimativamente il valore della funzione nel punto considerato, ad esempio

f

(x

i). Dallo schema, è evidente che quanto più piccole sono le strisce più adatte alle strisce all'interno dell'area limitata, quindi una migliore approssimazione del valore. Quindi, in generale, l'intero definito _I , tra i punti a e b (i. E nell'intervallo [a, b] dove a

I ≅ f (X ) Δx + n) Δx, dove n è il numero di strisce (n = (ba) / Δx).Questa sommazione dell'area può essere facilmente rappresentata utilizzando la notazione di somma come I _{≅ Σ < n} (x i) Δx Poiché l'approssimazione è migliore quando Δx è più piccolo, possiamo calcolare il valore quando Δx → 0, Quindi è ragionevole dire _{Δx → 0} Σ n i = 1 ^f _(x i) Δx. _{Come generalizzazione dal concetto sopra, possiamo scegliere la Δx basata sull'intervallo considerato indicizzato da i (scegliendo la larghezza dell'area in base alla posizione) I} = lim Δx → 0 Σ _n i = 1 ^f _(x i) Δx < > i ₌ a

∫

b f _{(x) dx} Questo è noto come Reimann Integral funzione ^f _{(x) nell'intervallo [a, b]. In questo caso a e b sono conosciuti come il limite superiore e quello inferiore dell'integrale. L'integrazione di Reimann è una forma di base di tutti i metodi di integrazione.} In sostanza, l'integrazione è la somma dell'area quando la larghezza del rettangolo è infinitesimale. Qual è la differenza tra Integration e Summation? _{• La somma è l'aggiunta di una sequenza di numeri. Di solito, la somma è data in questo formato Σ} n _{i = 1} a _i quando i termini della sequenza hanno un pattern e possono essere espressi usando un termine generale. ^{• L'integrazione è fondamentalmente l'area delimitata dalla curva della funzione, dell'asse e dei limiti superiori e inferiori. Questa area può essere data come somma di aree molto più piccole incluse nell'area limitata.} • La somma coinvolge i valori discreti con i limiti superiori e inferiori, mentre l'integrazione coinvolge valori continui. • L'integrazione può essere interpretata come una forma speciale di sommatoria.

• Nei metodi di calcolo numerico, l'integrazione viene sempre eseguita come una sintesi.