Differenza tra parallelo e quadrilatero: parallelo al quadrilatero

Parallelogramma vs Quadrilaterale < Quadrilaterali e parallelogrammi sono poligoni trovati nella geometria euclidea. Il parallelogramma è un caso speciale del quadrilatero. I quadrilaterali possono essere piani (2D) o 3 Dimensional mentre i parallelogrammi sono sempre planari.

Quadrilatero

Quadrilatero è un poligono a quattro lati. Ha quattro vertici e la somma degli angoli interni è 3600 (2π rad). I quadrilaterali sono classificati in categorie autolivellanti e semplici quadrilatero. I quadrilateri che si intersecano hanno due o più fianchi che attraversano l'uno all'altro, e figure geometriche più piccole (come i triangoli si formano all'interno del quadrilatero).

I semplici quadrilaterali sono inoltre divisi in quadrilateri convessi e concavi. I quadrilateri concavi hanno lati adiacenti che formano angoli riflessi all'interno della figura. I quadrilateri semplici che non hanno angoli reflex internamente sono quadrilateri convessi. I quadrilaterali convessi possono sempre avere tessellazioni.

Una parte importante della geometria dei quadrilaterali ai livelli iniziali riguarda i quadrilateri convessi. Alcuni quadrilaterali ci conoscono molto dai giorni delle scuole elementari. Di seguito è riportato un diagramma che mostra diversi quadrilaterali convessi.

Parallelo

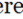
Il parallelo può essere definito come la figura geometrica con quattro lati, con lati opposti paralleli tra loro. Più precisamente è un quadrilatero con due coppie di parallele. Questa natura parallela dà molte caratteristiche geometriche ai parallelogrammi.

Un quadrilatero è un parallelogramma se si trovano le seguenti caratteristiche geometriche.

• Due coppie di lati opposti sono uguali in lunghezza. (AB = DC, AD = BC)

• Due coppie di angoli opposti sono uguali. ()

• Se gli angoli adiacenti sono supplementari

• Un paio di fianchi che si oppongono reciprocamente è parallelo e uguale in lunghezza. (AB = DC & AB∥DC)

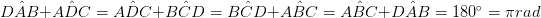
• Le diagonali si contraddicono a vicenda (AO = OC, BO = OD)

• Ogni diagonale divide il quadrilatero in due triangoli congruenti. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

Inoltre, la somma dei quadrati dei lati è uguale alla somma dei quadrati delle diagonali. Questo è talvolta definito come la legge

parallelogram e ha applicazioni diffuse in fisica e ingegneria. (AC 2 ^{= AC} 2 ^{+ BD} 2 ^{+ CD} 2 < 2 ⁾ Ciascuna delle caratteristiche sopra descritte può essere usata come proprietà, una volta stabilito che il quadrilatero è un parallelogramma. ^{L'area del parallelogramma può essere calcolata dal prodotto della lunghezza di un lato e dall'altezza al lato opposto. Pertanto, l'area del parallelogramma può essere indicata come} Area di parallelogramma = base × altezza = ^AB ×

h

L'area del parallelogramma è indipendente dalla forma del parallelogramma individuale. Dipende solo dalla lunghezza della base e dall'altezza perpendicolare.

Se i lati di un parallelogramma possono essere rappresentati da due vettori, l'area può essere ottenuta per la grandezza del prodotto vettoriale (prodotto incrociato) dei due vettori adiacenti. Se i lati AB e AD sono rappresentati rispettivamente dai vettori () e (), l'area del parallelogramma è data da

, dove α è l'angolo tra

e.

Di seguito sono riportate alcune proprietà avanzate del parallelogramma;

• L'area di un parallelogramma è due volte l'area di un triangolo creato da una delle sue diagonali.

• L'area del parallelogramma è divisa in metà da qualsiasi linea che passa attraverso il punto medio.

• Qualsiasi trasformazione affinica non degenerata assume un parallelogramma ad un altro parallelogramma

• Un parallelogramma ha simmetria di rotazione dell'ordine 2

• La somma delle distanze da qualsiasi punto interno di un parallelogramma ai lati è indipendente la posizione del punto

Qual è la differenza tra Parallelogramma e Quadrilatero?

• Quadrilaterali sono poligoni con quattro lati (a volte chiamati tetragoni) mentre il parallelogramma è un tipo speciale di un quadrilatero.

• I quadrilaterali possono avere i loro lati in piani diversi (nello spazio 3d) mentre tutti i lati del parallelogramma si trovano sullo stesso piano (planare / 2dimensionale).

• Gli angoli interni del quadrilatero possono assumere qualsiasi valore (compresi gli angoli di riflessione) in modo che aggiungano fino a 3600. I parallelogrammi possono avere solo angoli obbliq come il tipo massimo di angolo.

• Quattro lati del quadrilatero possono essere di lunghezze diverse mentre i lati opposti del parallelogramma sono sempre paralleli tra loro e uguali in lunghezza.

• Ogni diagonale divide il parallelogramma in due triangoli congruenti, mentre i triangoli formati dalla diagonale di un quadrilatero generale non sono necessariamente congruenti.