Differenza tra integrale definito e indefinito La differenza tra
Il calcolo è un ramo importante della matematica e la differenziazione gioca un ruolo fondamentale nel calcolo. Il processo inverso della differenziazione è noto come integrazione, e l'inverso è noto come integrale, o semplicemente put, l'inverso della differenziazione dà un integrale. Sulla base dei risultati che producono gli integrali sono divisi in due classi vale a dire. integrali definiti e indefiniti.
Definito integrale
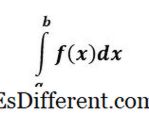
L'integrale definito di f (x) è un NUMERO e rappresenta l'area sotto la curva f (x) da x = a a x = b .
Un integrale definito ha limiti superiori e inferiori sugli integrali, ed è definito definito perché, alla fine del problema, abbiamo un numero - è una risposta definita.
Integrale indefinito

L'integrale indefinito di f (x) è una FUNZIONE e risponde alla domanda, "Quale funzione se differenziata dà f (x) ? "
Con un integrale indefinito non ci sono limiti superiori e inferiori sull'integrale qui, e quello che otterremo è una risposta che contiene ancora x e avrà anche una costante (di solito indicato con C ) in esso.
L'integrale indefinito di solito fornisce una soluzione generale all'equazione differenziale.
L'integrale indefinito è più di una forma generale di integrazione e può essere interpretato come l'anti-derivato della funzione considerata.
Supponiamo che la differenziazione della funzione F porti ad un'altra funzione f , e l'integrazione di f dà l'integrale. Simbolicamente, questo è scritto come
F (x) = ∫ƒ (x) dx
o
F = ∫ƒ dx
dove entrambi F e ƒ < sono funzioni di x e F sono differenziabili. Nella forma sopra, è chiamato un integrale di Reimann e la funzione risultante accompagna una costante arbitraria. Un integrale indefinito produce spesso una famiglia di funzioni; quindi, l'integrale è indefinito.
Integrali e processo di integrazione sono alla base della risoluzione di equazioni differenziali. Tuttavia, a differenza delle fasi di differenziazione, le fasi di integrazione non seguono sempre una routine chiara e standard. Occasionalmente, vediamo che la soluzione non può essere espressa esplicitamente in termini di funzione elementare. In tal caso, la soluzione analitica viene spesso data sotto forma di un integrale indefinito.
Teorema fondamentale del calcolo
L'integrale definito e l'indefinito sono collegati dal Teorema fondamentale del calcolo come segue: Per calcolare un
integrale definito , trova l'integrale indefinito > (noto anche come anti-derivato) della funzione e valutare sui punti finali x = a e x = b . La differenza tra integrali definiti e indefiniti sarà evidente una volta che valuteremo gli integrali per la stessa funzione. Considerare il seguente integrale:
OK. Facciamo entrambi e vediamo la differenza.
Per l'integrazione, è necessario aggiungerne uno all'indice che ci porta alla seguente espressione:

A questo punto del tempo
C
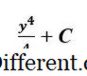
è semplicemente una costante per noi. Ulteriori informazioni sono necessarie nel problema per determinare il valore preciso di C . Valutiamo lo stesso integrale nella sua forma definita i. e., con i limiti superiore e inferiore inclusi. Graficamente parlando, stiamo calcolando l'area sotto la curva
f (x) = y

3 tra y = 2 e y = 3 >. Il primo passo in questa valutazione è lo stesso della valutazione integrale indefinita. L'unica differenza è che questa volta non aggiungiamo la costante C .
L'espressione in questo caso appare come segue: Questo è il turno che conduce a: Essenzialmente, abbiamo sostituito 3 e poi 2 nell'espressione e ottenuto la differenza tra loro.
Questo è il valore definito piuttosto che l'uso costante di

C

precedente.
Analizziamo il fattore costante (rispetto all'integrale indefinito) in maggior dettaglio. Se il differenziale di y
3
è 3y 2 , quindi ∫ 3y 2
dy = y 3 Tuttavia, 3y 2
potrebbe essere il differenziale di molte espressioni, alcune delle quali includono y 3 -5 , > y 3 +7 , ecc. Ciò implica che l'inversione non è unica poiché la costante non viene rilevata durante l'operazione. Quindi, in generale, 3y 2 è il differenziale di
y 3 + C dove C è una costante. Per inciso, C è noto come 'costante di integrazione' . Scriviamo come: ∫ 3y 2
. dx = y
3 + C Le tecniche di integrazione per un integrale indefinito, come la ricerca tabella o l'integrazione Risch, possono aggiungere nuove discontinuità durante il processo di integrazione. Queste nuove discontinuità appaiono perché gli anti-derivati possono richiedere l'introduzione di logaritmi complessi. I logaritmi complessi hanno una discontinuità di salto quando l'argomento attraversa l'asse reale negativo e gli algoritmi di integrazione a volte non riescono a trovare una rappresentazione dove questi salti si annullano.


