Differenza tra parallelogramma e rhombus: parallelogramma vs rhombus
Parallelogramma vs rhombus
Parallelogramma e rombo sono quadrilaterali. La geometria di queste figure è stata conosciuta dall'uomo da migliaia di anni. Il soggetto è trattato esplicitamente nel libro "Elementi" scritti dal matematico greco Euclid.
Parallelo
Il parallelogramma può essere definito come la figura geometrica con quattro lati, con lati opposti paralleli tra loro. Più precisamente è un quadrilatero con due coppie di parallele. Questa natura parallela dà molte caratteristiche geometriche ai parallelogrammi.

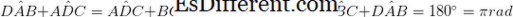
Un quadrilatero è un parallelogramma se si trovano le seguenti caratteristiche geometriche.
• Due coppie di lati opposti sono uguali in lunghezza. (AB = DC, AD = BC)
• Due coppie di angoli opposti sono uguali. (
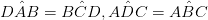
• Se gli angoli adiacenti sono supplementari
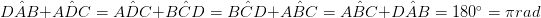
• Un paio di fianchi che si oppongono reciprocamente è parallelo e uguale in lunghezza. (AB = DC & ABáshozDC)
• Le diagonali si contraggono a vicenda (AO = OC, BO = OD)
Ogni diagonale divide il quadrilatero in due triangoli congruenti. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)
Inoltre, la somma dei quadrati dei lati è uguale alla somma dei quadrati delle diagonali. Questo è talvolta definito come la legge parallelogram e ha applicazioni diffuse in fisica e ingegneria. (AC 2 = AC 2 + BD 2 + CD 2 < 2 ) Ciascuna delle caratteristiche sopra descritte può essere usata come proprietà, una volta stabilito che il quadrilatero è un parallelogramma. L'area del parallelogramma può essere calcolata dal prodotto della lunghezza di un lato e dall'altezza al lato opposto. Pertanto, l'area del parallelogramma può essere indicata come Area del parallelogramma = base × altezza = AB × h L'area del parallelogramma è indipendente dalla forma del parallelogramma individuale. Dipende solo dalla lunghezza della base e dall'altezza perpendicolare.
Se i lati di un parallelogramma possono essere rappresentati da due vettori, l'area può essere ottenuta per la grandezza del prodotto vettoriale (prodotto incrociato) dei due vettori adiacenti.
Se i lati AB e AD sono rappresentati rispettivamente dai vettori () e (
 ), l'area del parallelogramma è data da, dove α è l'angolo tra
), l'area del parallelogramma è data da, dove α è l'angolo tra
e.





• La somma delle distanze da qualsiasi punto interno di un parallelogramma ai lati è indipendente la posizione del punto
Rhombus
Un quadrilatero con tutti i lati è uguale in lunghezza è conosciuto come un rombo. Viene anche chiamato come un quadrilatero equilaterale
. È considerato una forma di diamante simile a quella delle carte da gioco.
Il Rhombus è anche un caso speciale del parallelogramma. Può essere considerato come un parallelogramma con tutti e quattro i lati uguali. E ha le seguenti proprietà speciali, oltre alle proprietà di un parallelogramma.
• Le diagonali del rombo si susseguono a vicenda in angoli retti; le diagonali sono perpendicolari.
• Le diagonali dividono i due angoli interni opposti. • Almeno due dei lati adiacenti sono uguali in lunghezza. L'area del rombo può essere calcolata con lo stesso metodo del parallelogramma.


Qual è la differenza tra Parallelogramma e Rhombus?
• Parallelogramma e rombo sono quadrilaterali. Il Rhombus è un caso speciale dei parallelogrammi.
• L'area di qualsiasi può essere calcolata utilizzando la formula base × altezza.
• Considerando le diagonali;
- Le diagonali del parallelogramma si contraddicono a vicenda e bisettono il parallelogramma a formare due triangoli congruenti.
- Le diagonali del rombo si contraddicono a vicenda in angoli retti, ei triangoli formati sono equilaterali.
• Considerando gli angoli interni;
- Gli angoli interni opposti al parallelogramma sono uguali. Due angoli interni adiacenti sono complementari.
- Gli angoli interni del rombo sono bisettati dalle diagonali.
• Considerando i lati;
- In un parallelogramma, la somma dei quadrati dei lati è uguale alla somma dei quadrati della diagonale (Parallelogram law).
- Poiché tutti e quattro i lati sono uguali in un rombo, quattro volte il quadrato di un lato è uguale alla somma dei quadrati della diagonale.



